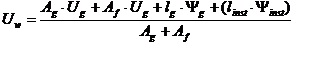О возможности использования контрольных карт Шухарта для управления производством ПВХ -окон
Традиционный подход к оценке производственных процессов, в том числе производства ПВХ – окон - это контроль качества результатов процесса после его реализации. Такая методика часто приводит к потерям и непригодна, поскольку основана на проверке пост-фактум, когда результаты, в том числе некачественные, уже “произведены”. Более эффективен подход предупреждения потерь, позволяющий избежать достижения некачественных результатов процессов. Такой подход предполагает сбор информации о самих процессах, ее анализ и результативные действия по отношению к ним, а не к конечным результатам. Одним из лучших способов решения этой задачи является статистический подход с использованием контрольных карт Шухарта (ККШ).
Контрольная карта Шухарта - это инструмент, важность которого для управления процессами, в первую очередь технологическими, была впервые показана американским ученым Шухартом в 1924 г.
Данная статья написана на основе идей книги Дональда Уиллера, Дэвида Чамберса “ Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. Пер. с англ. – М.: Альпина Бизнес Букс, 2009 “ и посвящена оценке возможности использования ККШ для управления производством ПВХ – окон.
В статье приведены общие сведения о методе ККШ – назначении и области использования, а также принципах составления ККШ и анализа. Приведены примеры использования контрольных карт для количественных и альтернативных показателей результативности применительно к некоторым процессам производства ПВХ – окон.
Содержание
- 1 Основы применения контрольных карт Шухарта
- 1.1 Основные обозначения и сокращения
- 1.2 Назначение и область применения ККШ.
- 1.3 Принципы составления и анализа ККШ.
- 1.4 Виды контрольных карт.
- 1.5 Последовательность расчета ККШ для количественных характеристик.
- 1.6 Последовательность расчета ККШ для альтернативных данных.
- 1.7 Подход к управлению производственными процессами на основе анализа ККШ для количественных данных.
- 1.8 Управление производственным процессом и оценка возможностей процесса
- 1.9 Планирование применения ККШ.
- 1.10 Примеры использования ККШ для количественных данных.
- 1.11 Примеры ККШ для альтернативных данных.
- 2 Примечание
- 3 Вклад участника
Основы применения контрольных карт Шухарта
Основные обозначения и сокращения
n - объем подгруппы, число выборочных измерений в подгруппе;
k - число подгрупп;
X - измеряемая характеристика качества процесса (индивидуальные значения записываются как
(X1,X2,X3 +)). Иногда вместо X используют Y ;
Ẋ - среднее значение для подгруппы,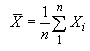 ;
;
Ẍ - среднее средних значений подгрупп;
μ - истинное среднее процесса;
Me - медиана подгруппы. Для выборки объема , значения , , которой упорядочены по возрастанию или по убыванию, медиана есть центральное значение, если нечетно, и среднее двух центральных значений, если четно;
R - размах подгруппы (разность наибольшего и наименьшего значений в подгруппе);
Примечание - В случае контрольной карты индивидуальных наблюдений R представляет собой скользящий размах, то есть абсолютную разность двух последовательных значений |X1-X2|, |X2-X3| и т.д.
![]() - среднее значение R для всех подгрупп;
- среднее значение R для всех подгрупп;
s - выборочное стандартное (среднее квадратическое) отклонение 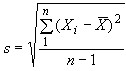 ;
;
![]() - среднее выборочных стандартных (средних квадратических) отклонений подгрупп;
- среднее выборочных стандартных (средних квадратических) отклонений подгрупп;
σ - истинное внутригрупповое стандартное отклонение;
![]() - оцененное внутригрупповое стандартное отклонение процесса;
- оцененное внутригрупповое стандартное отклонение процесса;
пр - число несоответствующих единиц в подгруппе;
p - доля несоответствующих единиц в подгруппе
![]() - среднее значение доли несоответствующих единиц
- среднее значение доли несоответствующих единиц
c - число несоответствий в подгруппе;
![]() - среднее значений с для всех подгрупп;
- среднее значений с для всех подгрупп;
u - число несоответствий на единицу в подгруппе;
![]() - среднее значение u
- среднее значение u![]()
CL - центральная линия;
UCL - верхняя контрольная граница;
LCL - нижняя контрольная граница.
Назначение и область применения ККШ.
ККШ являются одним из основных инструментов статистического управления процессами (СУП).
Статистическое управление процессами – это управление, основанное на измерении отклонений (вариации) результатов процесса и принятии решения о воздействии на процесс в зависимости от причин вариации. Основное назначение СУП – обеспечение управляемости и стабильности процессов, гарантируя соответствие результата процессов установленным требованиям (стандартам). Кроме того, ККШ можно использовать для назначения статистически обоснованных нормативных значений результатов процесса, а также аттестации технологических операций и оборудования.
Использование ККШ и их постоянный анализ ведут к лучшему пониманию и совершенствованию производственных процессов.
Известно, что точно предсказать результат практически всех процессов невозможно в принципе. Поэтому достаточно научиться прогнозировать результаты с такой точностью, которая экономически выгодна на данном уровне последствий принимаемых решений. Это можно сделать, если учесть, что большая часть результатов любого процесса определяется системой, в которой проходит этот процесс, и лишь небольшая их часть вызвана внешними причинами. Так, американский специалист Джозеф Джуран считал, что 85% результата обусловлено поведением системы и только 15% зависят, например, от поведения сотрудников системы или от качества входного сырья. Идеолог “японского экономического чуда” Эдвард Деминг утверждал о соотношении 98% / 2 % , оставляя внешним причинам всего 2% воздействий.
В связи с этим прежде всего надо научиться определять, какие результаты принадлежат системе, а какие – внешним или внутренним внесистемным силам. Результатами, обусловленными системой, можно управлять, только изменяя саму систему. Но сначала надо устранить все внесистемные воздействия, поскольку они неуправляемы, непредсказуемы.
В настоящее время распознавание воздействий, принадлежащих или не принадлежащих системе, производится с помощью ККШ. Шухарт предложил концепцию статистического управления процессами. Суть ее в следующем. Если система ( т.е. совокупность элементов, определяющих результаты производственного процесса) находится в стабильном, управляемом состоянии, то она ведет себя так, что ее результаты можно прогнозировать с определенной точностью до тех пор, пока кто-то (что-то) не выведет ее из этого состояния. Такая система была названа статистически управляемой. Именно прогнозируемость (предсказуемость) результата системы позволяет управлять процессом, а значит, улучшать его. Без предсказуемости улучшение процесса невозможно.
Если же есть какие-то внешние вмешательства в систему, то прогнозирование затрудняется, система становится не только непредсказуема, но и неуправляема. В этом случае надо устранить внешний источник вмешательства и вернуть систему в управляемое состояние. Значит необходимо научиться различать состояния, в которых находится система, а затем решать, что и кому надо с ней сделать (или не делать). ККШ позволяют ответить на вопрос: надо или не надо вмешиваться в систему, а если надо, то кому? Шухарт считал, что любые процессы подвержены вариабельности, но некоторые из них обладают управляемой вариацией, а некоторые – неуправляемой. Структура управляемой вариации стабильна и устойчива во времени, так как она вызвана действием многих независимых внутренне присущих данному процессу факторов. Схема примера такой управляемой вариации приведена на рис. 1, где в качестве результата процесса по оси абсцисс используется размер изделия (например, окна), а по оси ординат – частота каждого значения размера.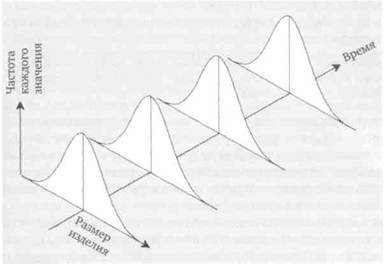
Рис. 1. Схема идеализированной управляемой вариации
Если на результаты процесса воздействуют внешние причины, не присущие данному процессу (например, разрегулировка станков, изменения в качестве входного сырья, различия в подготовке персонала и т.д.), то они приводят к существенным изменениям вариации результата процесса. Такая вариация называется неуправляемой.
Напр. посмотрим на процесс на Рис. 2. В первый период процесс стабилен. Во второй период измерений среднее измерений резко сместилось вверх. В третий период измерений среднее сместилось вниз. А в четвертый период измерений среднее осталось в норме, но резко выросло рассеяние. Именно наблюдая за поведением процесса с помощью карт, можно выявить изменения процесса и выявить внешние влияющие факторы. Такие внешние факторы, по мнению Шухарта, не только воздействуют на вариацию, но и снижают предсказуемость процесса. Он писал: “Явление следует называть управляемым тогда, когда , используя прошлый опыт, мы можем предсказать, по крайней мере в некоторых пределах, каких его вариаций можно ожидать в будущем ”.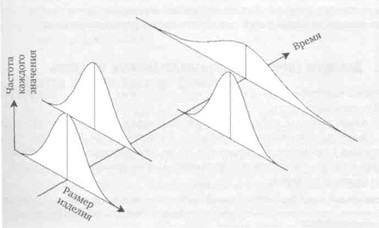
Рис. 2. Схема неуправляемой вариации
В соответствии с этими двумя типами производственных процессов существует два пути их улучшения :
- процесс с управляемой вариацией следует считать стабильным и устойчивым, а его улучшение состоит в снижении вариации и (или) изменении в лучшую сторону величины параметра результативности путем совершенствования самого процесса;
- процесс с неуправляемой вариацией является нестабильным и неустойчивым во времени, а его улучшение состоит, во-первых, в выявлении внешних возмущающих факторов, во-вторых, в устранении данных факторов (если они ухудшают процесс) или во встраивании данных факторов в процесс (если они улучшают процесс).
Поэтому, прежде чем улучшать процесс, следует определить, является ли его вариация управляемой или нет? Инструментом для обнаружения неуправляемой вариации являются ККШ, которые пригодны для обнаружения неуправляемой вариации любого процесса. Таким образом, ККШ являются инструментом постоянного совершенствования процессов, так как с их помощью выявляются внешние факторы, дестабилизирующие управляемый процесс.
Однако для правильного использования ККШ необходимы знания основных принципов их составления и анализа.
Принципы составления и анализа ККШ.
В общем случае алгоритм составления и анализа ККШ следующий.
- Предполагаем, что исследуемый процесс стабилен на протяжении времени, необходимого для сбора данных о результате процесса.
- Проводим сбор данных о результате процесса, выражаемым числовыми значениями выходного параметра.
- Предсказываем поведение средних значений и размахов результата процесса путем вычисления их контрольных пределов (нижних и верхних значений – на рис. 3, 4 показаны пунктирными линиями).
- Сравниваем наблюдаемые и предсказанные средние и размахи с контрольными пределами:
- если наблюдения согласуются с предсказаниями, процесс может быть стабильным , если процесс продолжает протекать в пределах рассчитанных границ и дальше, это доказывает его стабильность (см. рис.3);
- если наблюдения не согласуются с предсказаниями (значения результата не попадают в заданные пределы), процесс нестабилен,
выявляем и ликвидируем причины нестабильности (см. рис.4).
Рис. 3. Вид карты среднего (Х) и размаха ( R) для стабильного процесса 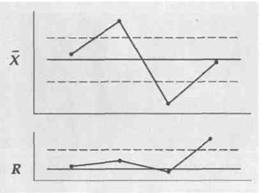
Рис. 4. Вид карты среднего (Х) и размаха ( R) для нестабильного процесса
Рассмотрим этот порядок подробнее. ККШ составляется на основе данных, получаемых не из всего процесса, а выборочно. Данные группируются в подгруппы (выборки). Желательно, чтобы каждая подгруппа состояла из однотипных изделий или услуг с одними и теми же показателями, и все подгруппы имели равные объемы (количество измерений). Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое подгруппы ![]() и размах подгруппы R или выборочное стандартное отклонение
и размах подгруппы R или выборочное стандартное отклонение ![]() . Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, установленное в технических условиях, или ее номинальное значение, основанное на предыдущей информации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (см. рис. 5).
. Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, установленное в технических условиях, или ее номинальное значение, основанное на предыдущей информации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (см. рис. 5).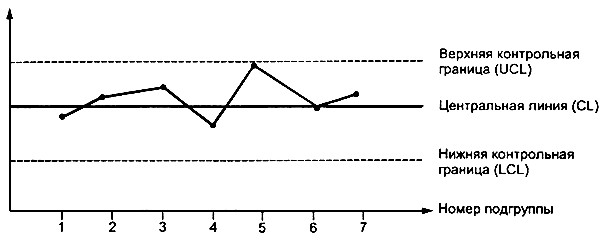
Рис. 5. Вид контрольной карты
Контрольные границы на карте Шухарта находятся на расстоянии 3 (три сигма) от центральной линии, где (сигма) - стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствующий коэффициент. Эта мера не включает межгрупповых вариаций, а оценивает только изменчивость внутри подгрупп.
Границы ±3 указывают, что около 99,7% значений характеристики подгрупп попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск, равный 0,3% (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен.
Вероятность того, что нарушение границ в самом деле случайное событие, а не реальный сигнал, считается столь малой, что при появлении точки вне границ следует предпринять определенные действия. Так как действие предпринимается именно в этой точке, то 3 контрольные границы иногда называются "границами действий".
Иногда на контрольной карте границы проводят еще и на расстоянии 2 . Тогда любое выборочное значение, попадающее за границы 2 , может служить предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Поэтому границы ±2 иногда называют "предупреждающими".
При применении ККШ возможны два вида ошибок: первого и второго рода.
Ошибка первого рода возникает, когда процесс находится в статистически управляемом состоянии, а точка выскакивает за контрольные границы случайно. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку найти и устранить причину несуществующей проблемы.
Ошибка второго рода возникает, когда рассматриваемый процесс не управляем, а точки случайно оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статистически управляем и упускают возможность предупредить выход некачественного изделия. Риск ошибки второго рода зависит от трех факторов: ширины контрольных границ, степени неуправляемости и объема выборки. Их природа такова, что можно сделать лишь общее утверждение о величине ошибки.
Система ККШ учитывает только ошибки первого рода, равные 0,3% в пределах границ 3 . Поскольку в общем случае сложно делать полную оценку потерь от ошибки второго рода в конкретной ситуации, а удобно произвольно брать малый объем подгруппы (4 или 5 единиц), целесообразно использовать границы на расстоянии ±3 и сосредоточивать внимание в основном на управлении и улучшении качества самого процесса.
Когда наносимое значение параметра выходит за любую из контрольных границ или серия значений проявляет необычные структуры, состояние статистической управляемости подвергается сомнению. В этом случае надо исследовать и обнаружить неслучайные (особые) причины, а процесс можно остановить или скорректировать. Как только особые причины найдены и исключены, процесс снова готов к продолжению работы. При возникновении ошибки первого рода можно не найти никакой особой причины. Тогда считают, что выход точки за границы представляет собой достаточно редкое случайное явление при нахождении процесса в статистически управляемом состоянии. Если контрольную карту процесса строят впервые, то часто оказывается, что процесс статистически неуправляем. Контрольные границы, рассчитанные на основе данных такого процесса, будут иногда приводить к ошибочным заключениям, поскольку они могут оказаться слишком широкими. Следовательно, прежде чем устанавливать постоянные параметры контрольных карт, надо привести процесс в статистически управляемое состояние.
Виды контрольных карт.
ККШ бывают двух основных типов: для количественных (непрерывных) и альтернативных (дискретных) данных. Количественные данные представляют собой наблюдения, полученные с помощью измерения и записи значений параметров для каждой единицы, рассматриваемой в подгруппе, например длина в метрах, вес в килограммах, шум в децибелах и т.д. Альтернативные (дискретные) данные представляют собой наблюдения, фиксирующие результаты подсчета чего-либо – например, числа дефектов какого-либо изделия или числа бракованных изделий в проверенной партии и т.д. Альтернативные данные в общем случае могут быть получены быстро и дешево, для сбора их не требуется специального обучения.
Для каждой контрольной карты встречаются две ситуации:
а) стандартные значения параметра процесса не заданы;
б) стандартные значения параметра процесса заданы.
Стандартные значения – это такие значения, которые определены системой в соответствии с требованиями (стандартами) или целями. Если стандартные значения не заданы, то цель таких карт - обнаружение отклонений значений параметров (например,![]() ,R или какой-либо другой статистики), которые вызваны не присущими процессу причинами. Эти контрольные карты основаны целиком на данных самих выборок.
,R или какой-либо другой статистики), которые вызваны не присущими процессу причинами. Эти контрольные карты основаны целиком на данных самих выборок.
В случае, если заданы стандартные значения, то целью таких карт является определение того, отличаются ли наблюдаемые значения ![]() ,R и т.п. для нескольких подгрупп (каждая объемом n наблюдений) от соответствующих стандартных значений xо (или μ ) и т.п. больше, чем можно ожидать при действии только присущих процессу причин. Особенностью карт с заданными стандартными значениями является дополнительное требование, относящееся к положению центра и вариации процесса. Установленные значения могут быть основаны на опыте, полученном при использовании контрольных карт без априорной информации, или на заданных стандартных значениях, а также на экономических показателях, установленных после рассмотрения потребности в услуге и стоимости производства, или указаны в технических требованиях на продукцию.
,R и т.п. для нескольких подгрупп (каждая объемом n наблюдений) от соответствующих стандартных значений xо (или μ ) и т.п. больше, чем можно ожидать при действии только присущих процессу причин. Особенностью карт с заданными стандартными значениями является дополнительное требование, относящееся к положению центра и вариации процесса. Установленные значения могут быть основаны на опыте, полученном при использовании контрольных карт без априорной информации, или на заданных стандартных значениях, а также на экономических показателях, установленных после рассмотрения потребности в услуге и стоимости производства, или указаны в технических требованиях на продукцию.
Желательно, чтобы установленные значения определялись на основе исследования предварительных данных. Для эффективного использования ККШ стандартные значения должны быть сопоставимы с присущей процессу изменчивостью. Карты, основанные на таких стандартных значениях, особенно полезны для управления процессами и поддержания однородности продукции на желаемом уровне. Для контрольных карт, использующих количественные данные, предполагается нормальное распределение для вариаций внутри выборок.
Последовательность расчета ККШ для количественных характеристик.
Для количественных характеристик используются чаще всего следующие ККШ:
1) карты среднего ( ![]() ) и размахов (R) или выборочных стандартных отклонений (S);
) и размахов (R) или выборочных стандартных отклонений (S);
2) карта индивидуальных значений (X) и скользящих размахов (R).
Карты для количественных данных отражают состояние процесса через разброс (изменчивость от единицы к единице) и через расположение центра (среднее процесса). Поэтому контрольные карты для количественных данных почти всегда применяют и анализируют парами - одна карта для расположения и одна - для разброса. Наиболее часто используют пару ![]() - и R- карту. В Приложении (таблицы 1 и 2) приведены формулы расчета контрольных границ и коэффициенты для соответствующих карт первого типа.
- и R- карту. В Приложении (таблицы 1 и 2) приведены формулы расчета контрольных границ и коэффициенты для соответствующих карт первого типа.
Иногда для управления процессами нельзя измерить рациональные подгруппы. Время или стоимость, требуемые для измерения при одиночном наблюдении, столь велики, что проведение повторных наблюдений даже не рассматривают. Это обычно происходит, когда измерения дорогостоящие (например, при разрушающем контроле) или выход продукции все время относительно однороден. В других ситуациях нельзя получить более одного значения, например значение показателя партии исходных ПВХ-профилей, поэтому приходится управлять процессом на основе индивидуальных значений.
При использовании карт индивидуальных значений рациональные подгруппы для обеспечения оценки изменчивости внутри партии не применяют и контрольные границы рассчитывают на основе меры вариации, полученной по скользящим размахам обычно двух наблюдений. Скользящий размах - это абсолютное значение разности измерений в последовательных парах, т.е. разность первого и второго измерений, затем второго и третьего и т.д. На основе скользящих размахов вычисляют средний скользящий размах ![]() , который используют для построения контрольных карт. Также по всем данным вычисляют общее среднее
, который используют для построения контрольных карт. Также по всем данным вычисляют общее среднее ![]() . В Приложении (таблица 3) приведены формулы расчета контрольных границ для карт индивидуальных значений.
. В Приложении (таблица 3) приведены формулы расчета контрольных границ для карт индивидуальных значений.
Последовательность расчета ККШ для альтернативных данных.
Для альтернативных данных используют следующие основные карты:
1) карта долей несоответствующих единиц продукции (p) или карта числа несоответствующих единиц (nр);
2) карта числа несоответствий (c) или карта числа несоответствий, приходящихся на единицу продукции (u).
В Приложении (таблица 4) приведены формулы расчета контрольных границ для контрольных карт, использующих альтернативные данные.
В случае контрольных карт для количественных данных принято ведение пары контрольных карт: для управления средним и управления отклонением, так как исходное распределение предполагается нормальным и зависит от этих двух параметров. При использовании контрольных карт для альтернативных данных достаточно одной карты, так как предполагаемое распределение имеет только один независимый параметр - средний уровень. p - и np -карты основаны на биномиальном распределении, а c - и u -карты - на распределении Пуассона.
Расчеты для этих карт одинаковы, за исключением случаев непостоянства объема подгрупп. Когда объем подгрупп постоянен, для каждой подгруппы могут быть выбраны одни и те же контрольные границы. Если число контролируемых единиц в каждой подгруппе различно, должны быть рассчитаны контрольные границы отдельно для каждого объема подгруппы. Таким образом, np - и c-карты могут быть применены при постоянном объеме подгруппы, а p - и u -карты - в любой ситуации.
Когда объем подгруппы изменяется от выборки к выборке, для каждой подгруппы рассчитывают свои контрольные границы, при этом чем меньше объем подгруппы, тем шире полоса между этими границами, и наоборот. Если объем подгрупп меняется несущественно, то можно ограничиться одним набором контрольных границ, основанным на среднем объеме подгруппы. Для практических целей достаточно, если объемы подгрупп находятся в пределах ±25% целевого объема подгруппы.
Альтернативный порядок в том случае, если объем подгруппы меняется существенно - использование нормированных переменных.
Например, вместо значений наносят нормированные значения и
и 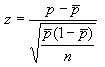
в зависимости от того, установлено или нет стандартное значение для P . Центральная линия и контрольные границы остаются постоянными независимо от объема подгруппы и выражаются следующим образом:
центральная линия равна 0,
UCL=3, LCL=3.
Обычно p-карту используют для определения среднего процента несоответствующих единиц, обнаруженных за определенный период времени. Она привлекает внимание к любым изменениям этого среднего. Процесс признается находящимся в состоянии статистической управляемости так же, как и при использовании ![]() - и R -карт. Если все выборочные точки ложатся внутри пробных контрольных границ без выбросов, то считают, что процесс управляем. В этом случае средняя доля несоответствующих
- и R -карт. Если все выборочные точки ложатся внутри пробных контрольных границ без выбросов, то считают, что процесс управляем. В этом случае средняя доля несоответствующих ![]() единиц берется как стандартное значение для доли несоответствующих единиц po .
единиц берется как стандартное значение для доли несоответствующих единиц po .
Подход к управлению производственными процессами на основе анализа ККШ для количественных данных.
Система карт Шухарта опирается на следующее условие: если изменчивость процесса от выборки к выборке и среднее процесса остаются постоянными на данных уровнях (оцененные, соответственно, по ![]() и
и ![]() ), то размахи R и средние
), то размахи R и средние ![]() отдельных подгрупп (выборок) будут меняться только случайным образом и редко выходить за контрольные границы. Не допускаются очевидные тренды или структуры данных, кроме возникающих случайно с некоторой долей вероятности.
отдельных подгрупп (выборок) будут меняться только случайным образом и редко выходить за контрольные границы. Не допускаются очевидные тренды или структуры данных, кроме возникающих случайно с некоторой долей вероятности.![]() - карта показывает, где находится среднее процесса и какова его стабильность. Та же карта выявляет нежелательные вариации между подгруппами и вариации относительно их среднего. R- карта выявляет любую нежелательную вариацию внутри подгрупп и служит индикатором изменчивости исследуемого процесса. Это мера состоятельности и однородности процесса. Если R-карта показывает, что вариации внутри подгрупп не изменяются, то это значит, что процесс остается в статистически управляемом состоянии. Такое происходит только в том случае, если все выборки обрабатывались одинаково. Если R -карта показывает, что процесс вышел из управляемого состояния или уровень на R -карте возрастает, то это может означать, что либо отдельные подгруппы подверглись разной обработке, либо в процессе действует несколько различных систем причинно-следственных связей.
- карта показывает, где находится среднее процесса и какова его стабильность. Та же карта выявляет нежелательные вариации между подгруппами и вариации относительно их среднего. R- карта выявляет любую нежелательную вариацию внутри подгрупп и служит индикатором изменчивости исследуемого процесса. Это мера состоятельности и однородности процесса. Если R-карта показывает, что вариации внутри подгрупп не изменяются, то это значит, что процесс остается в статистически управляемом состоянии. Такое происходит только в том случае, если все выборки обрабатывались одинаково. Если R -карта показывает, что процесс вышел из управляемого состояния или уровень на R -карте возрастает, то это может означать, что либо отдельные подгруппы подверглись разной обработке, либо в процессе действует несколько различных систем причинно-следственных связей.
На ![]() -карты также могут повлиять условия, при которых процесс вышел из состояния статистической управляемости по R -карте. Возможность интерпретировать размахи или средние подгрупп зависит от оценки изменчивости от единицы к единице, поэтому К -карту необходимо анализировать первой. Процедура управления следующая.
-карты также могут повлиять условия, при которых процесс вышел из состояния статистической управляемости по R -карте. Возможность интерпретировать размахи или средние подгрупп зависит от оценки изменчивости от единицы к единице, поэтому К -карту необходимо анализировать первой. Процедура управления следующая.
1) Собирают и анализируют данные, вычисляют средние и размахи.
2)Строят R-карту. Сопоставляют нанесенные точки размахов с контрольными границами, выделяют точки вне границ, необычные структуры или тренды. Для каждого сигнала о наличии неслучайной (внешней) причины в значениях размаха проводят анализ операций процесса, чтобы определить причину. Проводят корректирующие действия и действия по предотвращению повторения данной причины. 3) Исключают все подгруппы, на которые повлияла неслучайная причина, затем пересчитывают и наносят на карту новые средний размах R и контрольные границы. Необходимо получить подтверждение того, что все точки размахов при сравнении с новыми границами указывают на статистическую управляемость. Если требуется, повторяют последовательность действий "идентификация - корректировка - пересчет". 4) Если некоторые подгруппы исключены из R -карты из-за выявленных особых причин, их надо исключить и из ![]() -карты. Пересмотренные значения
-карты. Пересмотренные значения ![]() и
и ![]() надо использовать для пересчета пробных контрольных границ для средних.
надо использовать для пересчета пробных контрольных границ для средних.
5) Когда размахи находятся в статистически управляемом состоянии, разброс процесса (отклонения внутри подгрупп) считается стабильным. В этом случае можно проанализировать средние, чтобы увидеть, меняется ли со временем среднее положение процесса. 6) Теперь строят ![]() -карту и сравнивают точки с контрольными границами. Выделяют точки вне границ, необычные структуры точек или тренды. Также как и для R -карты необходимо анализировать любое из состояний статистической неуправляемости и проводить корректирующие и превентивные меры. Надо исключить точки, которые характеризуют это состояние и для которых были найдены неслучайные причины.
-карту и сравнивают точки с контрольными границами. Выделяют точки вне границ, необычные структуры точек или тренды. Также как и для R -карты необходимо анализировать любое из состояний статистической неуправляемости и проводить корректирующие и превентивные меры. Надо исключить точки, которые характеризуют это состояние и для которых были найдены неслучайные причины.
Повторно вычисляют и наносят на график новое среднее процесса (![]() ) и контрольные границы. Проверяют, чтобы, по сравнению с новыми границами, все точки демонстрировали статистически управляемое состояние, при необходимости возобновляя последовательные действия: "идентификация - корректировка - пересчет".
) и контрольные границы. Проверяют, чтобы, по сравнению с новыми границами, все точки демонстрировали статистически управляемое состояние, при необходимости возобновляя последовательные действия: "идентификация - корректировка - пересчет".
7) Если исходные данные для установления эталонных значений контрольных границ располагаются устойчиво внутри пробных пределов, расширяют границы, чтобы охватить будущие данные. Исполнители (оператор или мастер) должны пользоваться этими границами для последующего управления процессом, реагировать на сигналы о выходе процесса из управляемого состояния на любой из ![]() и R карт и выполнять надлежащие действия.
и R карт и выполнять надлежащие действия.
1.8. Критерии статистической управляемости процесса (наличия внешних причин)
Для анализа хода процесса по ККШ существует набор из восьми критериев, который схематически показан на рис. 6.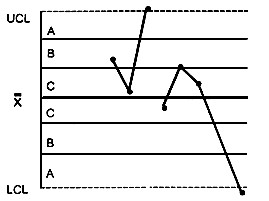
КРИТЕРИЙ 1 – Выход хотя - бы одной точки за трехсигмовые пределы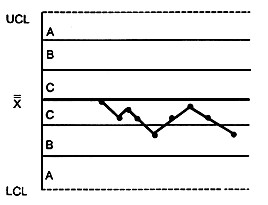
КРИТЕРИЙ 2 - Девять точек подряд в односигмовой зоне или по одну сторону от центральной линии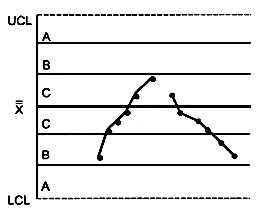
КРИТЕРИЙ 3 - Шесть возрастающих или убывающих точек подряд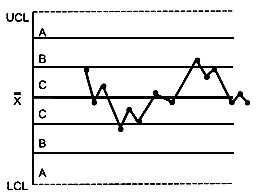
КРИТЕРИЙ 4 - Четырнадцать попеременно возрастающих и убывающих точек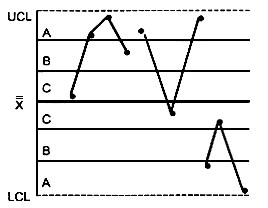
КРИТЕРИЙ 5 – Выход хотя- бы двух из трех последовательных точек, лежащих по одну сторону от центральной линии, за двухсигмовые пределы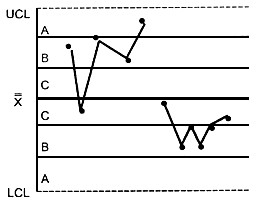
КРИТЕРИЙ 6 - Выход хотя - бы четырех из пяти последовательных точек, лежащих по одну сторону от центральной линии, за односигмовые пределы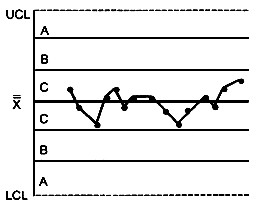
КРИТЕРИЙ 7 - Пятнадцать последовательных точек в односигмовой зоне выше и ниже центральной линии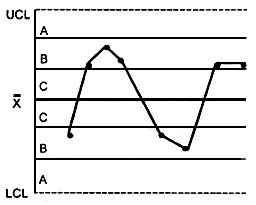
КРИТЕРИЙ 8 - Восемь последовательных точек по обеим сторонам центральной линии и ни одной в односигмовой зоне
Рис. 6. Критерии наличия особых причин в процессе
Этот набор критериев можно принять за основу, но следует обращать внимание на любую необычную структуру точек, которая может указывать на проявление особых (неслучайных) причин. Поэтому эти критерии следует рассматривать только как примеры ситуаций, когда может быть установлено проявление неслучайных причин. Появление любого из случаев, описанных в этих критериях, - указание на присутствие особых причин, которые должны быть проанализированы и скорректированы.
Верхняя и нижняя контрольные границы установлены на расстоянии 3σ над и под центральной линией. Для применения этих критериев контрольная карта делится на шесть равных зон шириной σ . Эти зоны обозначаются A, B, C, C , B, A, причем зоны расположены симметрично центральной линии. Данные критерии применимы к ![]() -картам и X-картам индивидуальных значений. Предполагается нормальное распределение соответственно
-картам и X-картам индивидуальных значений. Предполагается нормальное распределение соответственно ![]() и индивидуальных значений.
и индивидуальных значений.
Управление производственным процессом и оценка возможностей процесса
Управление производственным процессом состоит в выявлении сигнала о наличии особых (неслучайных) причин вариаций и систематическом их устранении, что приводит процесс в управляемое состояние. Возможности процесса определяются вариацией, обусловленной внутренне присущими процессу факторами (причинами), т.е. вариацией, которая остается после устранения всех неслучайных причин. Возможности процесса представляют показатели самого процесса в статистически управляемом состоянии, поэтому процесс сначала приводят в такое состояние, а затем определяют его возможности. Таким образом, определение возможностей процесса начинается после того, как задачи управления по - и - -картам решены, т.е. особые причины выявлены, проанализированы, скорректированы и их повторение предотвращено. Текущие контрольные карты должны демонстрировать сохранение процесса в статистически управляемом состоянии, по крайней мере, для 25 подгрупп. Далее разброс данных на выходе процесса сравнивается с требованиями стандарта для подтверждения того, что эти требования могут быть уверенно выполнены.
В общем случае возможности процесса определяют индексом возможностей процесса PCI (Cp):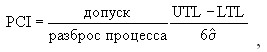
где UTL - верхнее предельно допустимое значение контролируемого параметра;
LTL - нижнее предельно допустимое значение контролируемого параметра;
ό - оценивают по средней изменчивости внутри подгрупп и выражают как ![]() или
или ![]() .
.
При меньше 1 возможности процесса неприемлемы, а при равном 1, процесс находится на грани требуемых возможностей. На практике в качестве минимально приемлемого значения берется = 1,33, поскольку всегда есть некоторые вариации в выборках, и нет процессов, которые всегда находятся в статистически управляемом состоянии.
Показатель настроенности (налаженности процесса) процесса PCK (Срк) характеризует возможные уровни несоответствий с учетом реальной настройки процесса, он определяется как минимальное значение из допустимого нижнего и верхнего полуразброса процесса (СРL и СРU соответственно):
СРL = (допустимый нижний полуразброс процесса) / (фактический нижний полуразброс процесса) = (Х - LTL ) / (3 х ![]() ); СРU = (допустимый верхний полуразброс процесса) / (фактический верхний полуразброс процесса) = (UTL - Х) / (3 х
); СРU = (допустимый верхний полуразброс процесса) / (фактический верхний полуразброс процесса) = (UTL - Х) / (3 х ![]() ); где Х – среднее значение показателя процесса. Порядок совершенствования процесса представлен на рис.7.
); где Х – среднее значение показателя процесса. Порядок совершенствования процесса представлен на рис.7.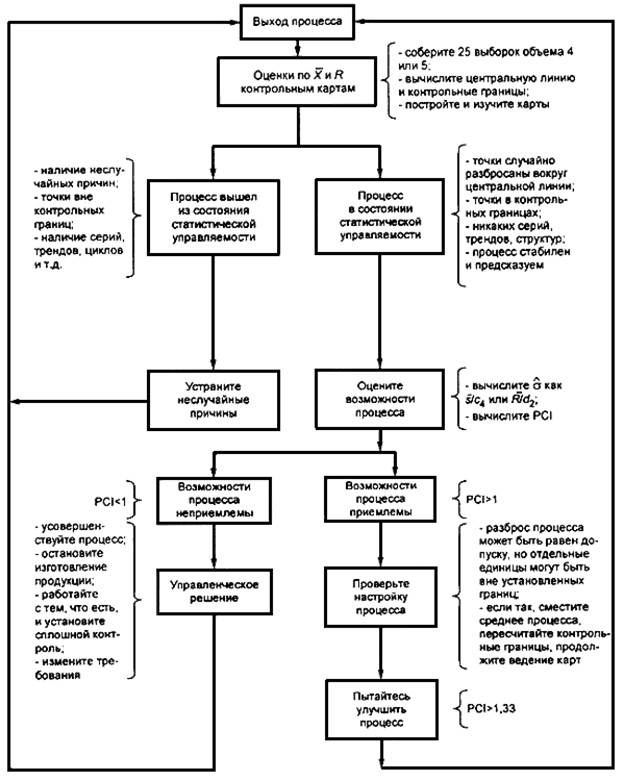
Рис. 7. Порядок улучшения производственного процесса
Планирование применения ККШ.
Прежде чем применять ККШ, необходимо выбрать показатели процесса, определить источники нестабильности и методы их устранения, выбрать рациональные подгруппы (выборки), определить объем и частоту выборок, а также сделать предварительный сбор данных. 1.9.1. Выбор показателей процесса.
В качестве показателей результативности процесса должны быть выбраны параметры, оказывающие решающее влияние на качество изделия (услуги) и обеспечение стабильности процессов.
Следует также установить, какие возможные причины могут быть источником нестабильности процесса, а также методы их устранения.
1.9.2. Выбор рациональных подгрупп (выборок)
В основе контрольных карт лежит идея Шухарта о разделении наблюдений на так называемые "рациональные" подгруппы, внутри которых могут возникнуть вариации, обусловленные только случайными (внутренне присущими процессу) причинами, в то время как различия между ними могут быть обусловлены особыми (внешними) причинами, которые контрольные карты и должны обнаружить.
Для этого необходимы определенные знания процесса и получения данных.
Следует соблюдать следующие основные принципы выбора подгрупп:
- вариация результата внутри подгрупп должна быть минимальной
- вариация между подгруппами должна быть максимальной.
1.9.3. Частота и объем подгрупп
Нет четких правил для определения частоты отбора подгрупп и их объемов. Частота может зависеть от стоимости взятия и анализа выборки, а объем подгрупп - от ряда иных соображений. Например, большие подгруппы, берущиеся с меньшей частотой, могут обнаружить малый сдвиг среднего процесса более точно, но малые подгруппы, берущиеся чаще, обнаруживают большие сдвиги быстрее. Часто объем подгруппы берется из 4 или 5 единиц, а частота отбора обычно выше в начале работы, чем при достижении состояния статистической управляемости. Обычно 20-25 подгрупп объема 4 или 5 рассматриваются как приемлемые для получения предварительных оценок.
Частота выборок, стабильность и возможности процесса должны рассматриваться совместно, так как для оценки σ часто используют среднее значение размаха ![]() , и количество источников вариаций увеличивается с ростом временного интервала между выборочными единицами внутри подгруппы. Поэтому увеличение времени между выборочными единицами в подгруппе увеличивает
, и количество источников вариаций увеличивается с ростом временного интервала между выборочными единицами внутри подгруппы. Поэтому увеличение времени между выборочными единицами в подгруппе увеличивает ![]() и оценку σ , расширяет контрольные границы и тем самым уменьшает индекс возможностей процесса.
и оценку σ , расширяет контрольные границы и тем самым уменьшает индекс возможностей процесса.
Напротив, можно увеличить индекс возможностей, выбрав последовательные единицы продукции, получая малые значения и оценки , но состояния статистической управляемости будет трудно достигнуть.
1.9.4. Предварительный сбор данных
После решения о выборе показателя результата процесса, который следует контролировать, частоты и объема подгрупп должны быть собраны и проанализированы некоторые первоначальные данные контроля или измерений, чтобы определить предварительные параметры контрольных карт: центральную линию и контрольные границы. Предварительные данные могут быть собраны последовательно, пока не будет получено 20-25 подгрупп при непрерывном ходе процесса. При их сборе важно, чтобы процесс не подвергался особым внешним влияниям, таким как изменения в подаче материалов, операциях, режимах станков и т.п. Другими словами, процесс должен быть достаточно стабилен в период сбора предварительных данных.
Примеры использования ККШ для количественных данных.
1.10.1. ![]() - и R -карты, стандартные значения заданы.
- и R -карты, стандартные значения заданы.
В процессе производства партии пластиковых окон производится резка армирующего профиля заданного размера, причем предъвляется требование, чтобы размер профиля в среднем был равен 100,6 см и стандартное отклонение размера было не более 1,4 см. Требуется оценить стабильность операции резки профиля с использованием имеющейся в цеху пилы с данной измерительной линейкой.
Поскольку стандартные значения заданы (Xо = 100,6; σо = 1,4), контрольную карту средних и карту размахов можно построить с использованием формул, приведенных в таблице 1 и коэффициентов A, d2, D2 и D1 , приведенных в таблице 2 для n= 5.![]() -КАРТА:
-КАРТА:
центральная линия: = 100,6 см
UCL=Xо+Aσо = 100,6 + (1,342 х 1,4) = 102,5 см
LCL=Xо-Aσо = 100,6 - (1,342 x 1,4) = 98,7 см
R -КАРТА:
центральная линия: d2σо = 2,326 х 1,4 = 3,3 см
UCL=D2σо= 4,918 х 1,4 = 6,9 см
LCL=D1σо= 0 х 1,4 = 0
(т.к. n < 7, то LCL отсутствует)
Для контроля процесса резки следует взять 25 выборок объема 5 резов каждая. Для примера значения их средних и размахов приведены в таблице 5, при этом каждые полчаса проводили измерения размеров пяти профилей и включали их в подгруппы. На рис. 8 значения средних и размахов нанесены вместе с контрольными границами.
Таблица 5
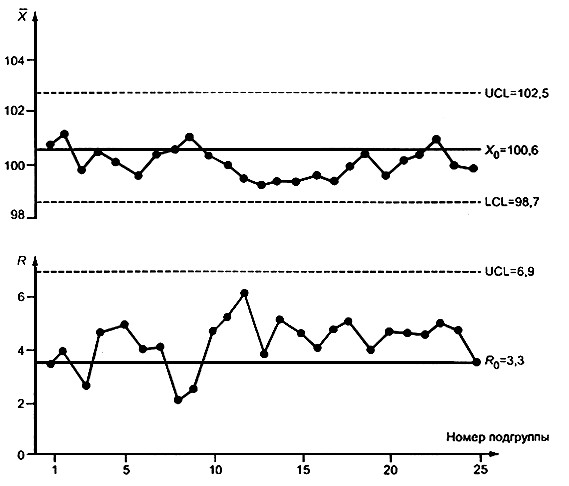
Рис. 8. Карты средних и размахов по данным таблицы 5
Карты, изображенные на рис. 8, показывают, что процесс не находится в статистически управляемом состоянии на требуемом уровне, так как есть последовательность из 13 точек (начиная с 10 подгруппы), лежащих ниже центральной линии на ![]() -карте и последовательность из 15 точек выше центральной линии на R -карте. Таким образом, карта показала, что через 5 часов работы появилась внешняя (не присущая данному процессу) причина, приводящая к систематическому уменьшению длины отрезаемого армирующего профиля ниже заданного в среднем размера. Причина столь длинной последовательности низких значений среднего должна быть выявлена и устранена.
-карте и последовательность из 15 точек выше центральной линии на R -карте. Таким образом, карта показала, что через 5 часов работы появилась внешняя (не присущая данному процессу) причина, приводящая к систематическому уменьшению длины отрезаемого армирующего профиля ниже заданного в среднем размера. Причина столь длинной последовательности низких значений среднего должна быть выявлена и устранена.
1.10.2. ![]() - и R- карты, стандартные значения не заданы.
- и R- карты, стандартные значения не заданы.
Со склада производителя пластиковых окон автомобильным транспортом производится отгрузка изделий дилерам. Вес одной пирамиды с изделиями, погружаемой на автомобиль, ограничен располагаемой трудоемкостью погрузочно - разгрузочных работ и экономической рентабельностью перевозки. В связи с этим вес погружаемых на каждую пирамиду изделий должен быть не менее 0, 125 т, но не более 0, 219т.
Требуется определить параметры процесса погрузки изделий на пирамиды и управлять им по настройке и разбросу так, чтобы он соответствовал установленным требованиям.
В таблице 6 приведены результаты измерений веса погружаемых на пирамиды изделий. В каждой подгруппе измерялся вес четырех пирамид, всего взято 20 выборок с периодичностью 4 часа. Средние и размахи подгрупп также приведены в таблице 6. Таблица 6.
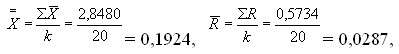
где k - число подгрупп, k = 20.
Первый шаг: построение R-карты и определение по ней состояния процесса.
R -КАРТА:
UCL=D4![]() = 2,282 х 0,0287 = 0,0655;
= 2,282 х 0,0287 = 0,0655;
LCL=D3![]() = 0 х 0,0287 = 0 (т.к. n < 7, то LCL отсутствует).
= 0 х 0,0287 = 0 (т.к. n < 7, то LCL отсутствует).
Значения множителей D3 и D4 взяты из таблицы 2 Приложения для = 4. Поскольку значения ![]() в таблице 6 находятся внутри контрольных границ,
в таблице 6 находятся внутри контрольных границ, ![]() -карта указывает на статистически управляемое состояние. Значение
-карта указывает на статистически управляемое состояние. Значение ![]() теперь может быть использовано для вычисления контрольных границ
теперь может быть использовано для вычисления контрольных границ ![]() -карты.
-карты.![]() -КАРТА.
-КАРТА.
UCL=![]() +A2
+A2![]() = 0,1924 + (0,729 x 0,0287) = 0,2133;
= 0,1924 + (0,729 x 0,0287) = 0,2133;
LCL=![]() -A2
-A2![]() = 0,1924 - (0,729 x 0,0287) = 0,1715.
= 0,1924 - (0,729 x 0,0287) = 0,1715.
Значение множителя A2 берется из таблицы 2 Приложения для n= 4.![]() и R-карты представлены на рис.9. Анализ
и R-карты представлены на рис.9. Анализ ![]() -карты показывает, что последние три точки вышли за границы. Это указывает на возможность действия некоторых особых причин вариаций. Если пределы были вычислены на основе предыдущих данных, то должно быть предпринято действие в точке, соответствующей 18-й подгруппе.
-карты показывает, что последние три точки вышли за границы. Это указывает на возможность действия некоторых особых причин вариаций. Если пределы были вычислены на основе предыдущих данных, то должно быть предпринято действие в точке, соответствующей 18-й подгруппе.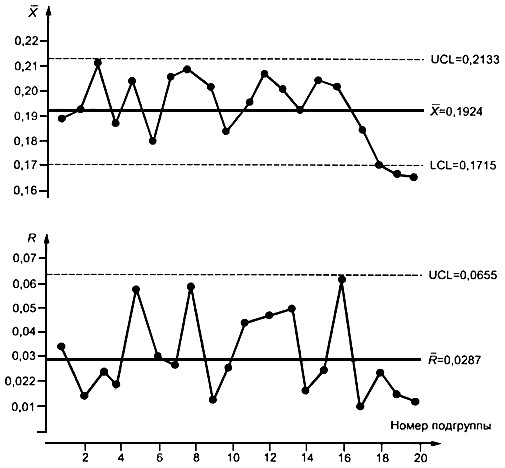
Рис. 9. Карты средних и размахов по данным таблицы 6
В этой точке процесса следует произвести соответствующее корректирующее действие, чтобы устранить особые причины и предотвратить их повторение. Работа с картами продолжается после установления пересмотренных контрольных границ без исключенных точек, которые вышли за старые границы, т.е. значений для выборок N 18, 19 и 20. Значения ![]() ,
, ![]() и линии контрольной карты пересчитывают следующим образом:
и линии контрольной карты пересчитывают следующим образом:
пересмотренное значение ![]() = 0,1968,
= 0,1968,
пересмотренное значение ![]() = 0,0310,
= 0,0310,
пересмотренная ![]() -карта имеет следующие параметры:
-карта имеет следующие параметры:
центральная линия: ![]() = 0,1968;
= 0,1968;
UCL=![]() +A2
+A2![]() = 0,1968 + (0,729 x 0,0310) = 0,2194;
= 0,1968 + (0,729 x 0,0310) = 0,2194;
LCL=![]() -A2
-A2![]() = 0,1966 - (0,729 x 0,0310) = 0,1742.
= 0,1966 - (0,729 x 0,0310) = 0,1742.
пересмотренная R-карта:
UCL=D4![]() = 2,282 x 0,0310 = 0,0707;
= 2,282 x 0,0310 = 0,0707;
LCL=D3![]() = 0 x 0,0310 = (т.к. n < 7, LCL отсутствует).
= 0 x 0,0310 = (т.к. n < 7, LCL отсутствует).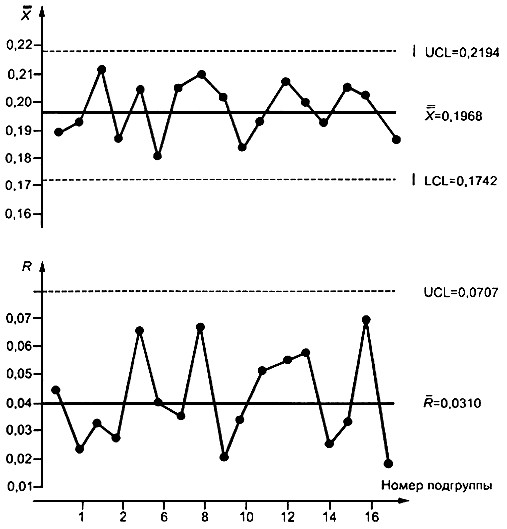
Рис. 10. Пересмотренные ![]() - и R -карты по данным таблицы 6
- и R -карты по данным таблицы 6
Для стабильного процесса с пересмотренными контрольными границами можно оценить возможности. Вычисляем индекс возможностей: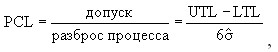
где ![]() оценивается как
оценивается как ![]() /d2 = 0,0310/2,059 = 0,0151;
/d2 = 0,0310/2,059 = 0,0151;
значение постоянной в 2 берется из таблицы 2 Приложения для n = 4.
Таким образом,![]()
Поскольку PCI больше 1, возможности процесса можно считать приемлемыми.
Вычислим показатели настроенности процесса СРL и СРU:
СРL = (допустимый нижний полуразброс процесса) / (фактический нижний полуразброс процесса) = (Х - LTL ) / (3 х ![]() );
);
СРL = (0.1968 – 0.125 ) / (3 х 0.0151) = 1.58;
СРU = (допустимый верхний полуразброс процесса) / (фактический верхний полуразброс процесса) = ( UTL - Х) / (3 х ![]() );
);
СРU = ( 0.2194 – 0.1968 ) / (3 х 0.0151) = 0.499;
РСК = MIN (СРL, СРU ) = 0.499.
Таким образом, показатель настроенности процесса РСК = 0.499 , а это означает, что процесс не настроен правильно относительно допуска и поэтому некоторое количество единиц будут выходить за установленное верхнее предельно допустимое значение UTL . Поэтому, прежде чем установить постоянные параметры контрольных карт, надо попытаться правильно настроить процесс, поддерживая его при этом в статистически управляемом состоянии.
1.10.3. Контрольные карты для индивидуальных значений X и скользящих размахов R , стандартные значения не заданы.
Требуется оценить за квартал процесс поставки комплектующих от поставщика на склад производителя пластиковых окон на предмет недопоставок - соответствия фактического количества артикулов заявленному.
В таблице 7 представлены результаты контроля, проведенного по выборкам из 10 последовательных поставок. Несоответствие артикулов Х в поставке определялось как отношение числа недопоставленных артикулов поставки к общему числу заявленных артикулов в поставке. Так как количество поставок за квартал ограничено, было решено установить контрольные границы на основе скользящего размаха последовательности поставок.
Таблица 7.
| Наименование показателя |
Значение для подгруппы | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Несоответствие артикулов X,% |
2.9 |
3.2 |
3.6 |
4.3 |
3.8 |
3.5 |
3.0 |
3.1 |
3.6 |
3.5 |
| Скользящий размах R |
|
0.3 |
0.4 |
0.7 |
0.5 |
0.3 |
0.5 |
0.1 |
0.5 |
0.1 |
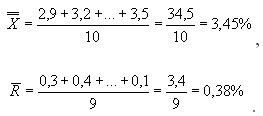
UCL=D4![]() = 3,267 х 0,38 = 1,24;
= 3,267 х 0,38 = 1,24;
LCL=D3![]() = 0 х 0,38 (т.к. n < 7, LCL отсутствует).
= 0 х 0,38 (т.к. n < 7, LCL отсутствует).
Значения множителей D3 и D4 берутся из таблицы 2 Приложения для n= 2. Поскольку карта размахов демонстрирует статистически управляемое состояние, можно построить контрольную карту индивидуальных значений.
Линии контрольной карты индивидуальных значений X:
центральная линия: ![]() = 3,45;
= 3,45;
UCL=![]() +E2
+E2 ![]() = 3,45 + (2,66 х 0,38) = 4,46;
= 3,45 + (2,66 х 0,38) = 4,46;
LCL=![]() +E2
+E2 ![]() = 3,45 - (2,66 х 0,38) = 2,44.
= 3,45 - (2,66 х 0,38) = 2,44.
Формулы для контрольных границ и значение коэффициента даны в таблицах 3, 4 Приложения. Контрольные карты приведены на рисунке 8. Они показывают, что процесс находится в состоянии статистической управляемости.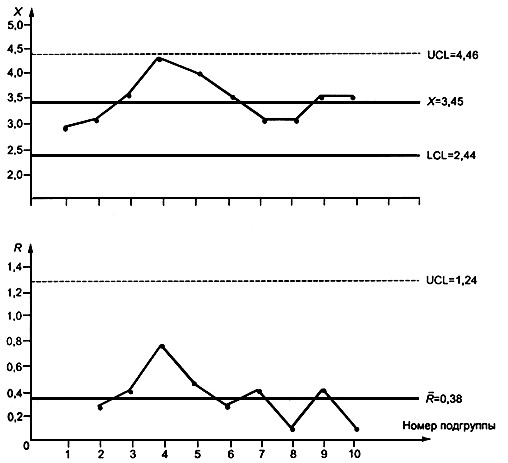
Рис. 8. Контрольная карта индивидуальных значений по данным, приведенным в таблице 7.
Примеры ККШ для альтернативных данных.
1.11.1. p -Карта. Стандартные значения не заданы. На производстве пластиковых окон было принято решение улучшить управление качеством операции нарезки штапика, для чего ввести карту доли несоответствующих единиц . Были собраны и проанализированы данные за 1 месяц. Ежедневно с периодичностью 1 час извлекались случайные выборки (подгруппы) и регистрировалось количество заготовок штапиков, несоответствующих заданному размеру. Данные приведены в таблице 8.
Таблица 8.
| Номер подгруппы |
Число проконтролированных единиц (штапиков) |
Число несоответствующих единиц np (штапиков) |
Доля несоответствующих единиц p (штапиков) |
UCL |
LCL |
|---|---|---|---|---|---|
| 1 | 158 | 11 | 0,070 | 0,117 | 0,003 |
| 2 | 140 | 11 | 0,079 | 0,120 | 0,000 |
| 3 | 140 | 8 | 0,057 | 0,120 | 0,000 |
| 4 | 155 | 6 | 0,039 | 0,177 | 0,003 |
| 5 | 160 | 4 | 0,025 | 0,116 | 0,004 |
| |
|
|
|
|
|
| 6 | 144 | 7 | 0,049 | 0,119 | 0,001 |
| 7 | 139 | 10 | 0,072 | 0,120 | 0,000 |
| 8 | 151 | 11 | 0,073 | 0,118 | 0,002 |
| 9 | 163 | 9 | 0,055 | 0,116 | 0,004 |
| 10 | 148 | 5 | 0,038 | 0,119 | 0,001 |
| |
|
|
|
|
|
| 11 | 150 | 2 | 0,013 | 0,118 | 0,002 |
| 12 | 153 | 7 | 0,046 | 0,118 | 0,002 |
| 13 | 149 | 7 | 0,047 | 0,118 | 0,002 |
| 14 | 145 | 8 | 0,055 | 0,119 | 0,001 |
| 15 | 160 | 6 | 0,038 | 0,116 | 0,004 |
| |
|
|
|
|
|
| 16 | 165 | 15 | 0,091 | 0,115 | 0,005 |
| 17 | 136 | 18 | 0,132 | 0,121 | 0,000 |
| 18 | 153 | 10 | 0,065 | 0,118 | 0,002 |
| 19 | 150 | 9 | 0,060 | 0,118 | 0,002 |
| 20 | 148 | 5 | 0,034 | 0,119 | 0,001 |
| |
|
|
|
|
|
| 21 | 135 | 0 | 0,000 | 0,121 | 0,000 |
| 22 | 165 | 12 | 0,073 | 0,115 | 0,005 |
| 23 | 143 | 10 | 0,070 | 0,120 | 0,000 |
| 24 | 138 | 8 | 0,058 | 0,121 | 0,000 |
| 25 | 144 | 14 | 0,097 | 0,119 | 0,001 |
| 26 | 161 | 20 | 0,124 | 0,116 | 0,004 |
| Всего | 3893 | 233 |
Средняя доля несоответствующих единиц за месяц подсчитывалась следующим образом:
Поскольку объемы подгрупп различны, значения UCL и LCL вычисляют для каждой подгруппы отдельно по формуле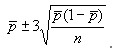
Значения UCL и LCL также приведены в таблице 8. Очевидно, что вычисление значений и построение линий UCL и LCL для каждой подгруппы достаточно трудоемко. Однако из таблицы 8 видно, что доли несоответствующих единиц для подгрупп N 11 и 26 не лежат в соответствующих пределах. Эти две подгруппы были исключены из данных, поскольку они подверглись другим неслучайным изменениям. Включение их в расчеты привело бы к завышению среднего и контрольных границ. Причины этих высоких значений должны быть найдены, чтобы предпринять соответствующие корректирующие действия для предотвращения их будущих появлений. Пересмотренная средняя доля несоответствующих единиц вычислена для значений остальных 24 подгрупп.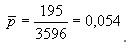
Подсчет UCL и LCL для каждой подгруппы с использованием пересмотренного значения выявляет, что все доли несоответствующих единиц находятся внутри соответствующих контрольных границ. Поэтому пересмотренное значение взято в качестве стандартной доли несоответствующих единиц для построения контрольных карт. Таким образом, pо = 0,054.
Как отмечалось выше, построение верхних контрольных границ для каждой подгруппы переменного объема - трудоемкий и кропотливый процесс. Однако поскольку объемы подгрупп не сильно отличаются от среднего объема выборки, равного 150, пересмотренная p- карта (с использованием po = 0,054) может быть построена с использованием верхней контрольной границы для среднего объема подгруппы, равного = 150. Тогда можно вычислить линии пересмотренной p-карта.
Пересмотренная p-карта:
центральная линия po = 0,054;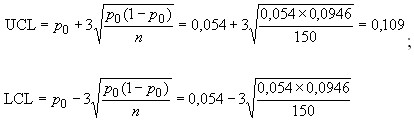
(так как отрицательные значения невозможны, нижняя граница отсутствует).
Карта на рисунке 8 показывает состояние статистической управляемости процесса.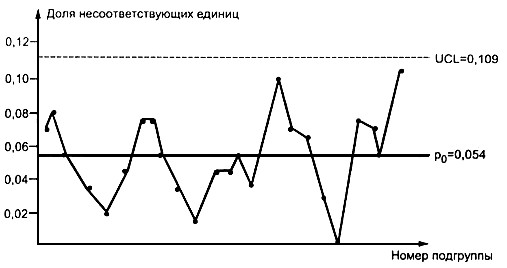
Рис. 8. Пересмотренная - Карта по данным таблицы 8.
1.11.1 u-Карта - число несоответствий на единицу.
Требуется определить стабильность операции сварки пластикового профиля с применением данной сварочной машины на предмет соответствия качества сварного шва требуемым техническим условиям. Для этого было решено применить u -карту для числа несоответствий на единицу. С этой целью каждый день контролировали 15 операций сварки профиля одинакового типа и определяли общее число несоответствий качества сварки и их число на единицу. Данные контроля качества сварки по 14 подгруппам, объемом n = 15 каждая приведены в таблице 9.
Таблица 9.
| Номер подгруппы |
Число несоответствий с |
Число несоответствий на единицу u |
|---|---|---|
| 1 | 4 | 0,27 |
| 2 | 5 | 0,33 |
| 3 | 3 | 0,20 |
| 4 | 6 | 0,40 |
| 5 | 2 | 0,13 |
| 6 | 1 | 0,07 |
| 7 | 5 | 0,33 |
| 8 | 6 | 0,40 |
| 9 | 2 | 0,13 |
| 10 | 4 | 0,27 |
| 11 | 7 | 0,47 |
| 12 | 5 | 0,33 |
| 13 | 2 | 0,13 |
| 14 | 3 | 0,20 |
| Всего | 55 |
Среднее значений u подсчитывалось из таблицы 9 делением общего числа несоответствий (из ряда c-значений) на общее число проконтролированных единиц (т.е. 14 х 15). ![]()
u-Карта:
центральная линия: ū = 0,26; 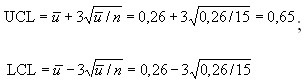
(т.к. отрицательные значения невозможны, нижняя граница отсутствует).
Данные и контрольные линии нанесены на рисунке 9. Карта показывает, что процесс находится в состоянии статистической управляемости и вмешиваться в него не следует.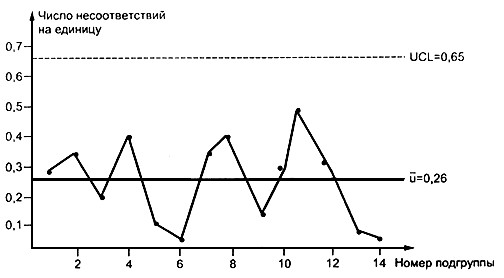
Рис.9. - u -Карта по данным таблицы 9
Таким образом, приведенные выше примеры показывают, что ККШ возможно использовать для статистического управления качеством процессов производства пластиковых окон. Для этого следует иметь рабочую группу специалистов, хорошо знающих процессы и имеющих необходимые знания в области статистики.
Примечание
- Дональд Уиллер, Дэвид Чамберс. Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. Пер. с англ. – М.: Альпина Бизнес Букс, 2009.
- Эдвард Деминг. Выход из кризиса: Новая парадигма управления людьми, системами и процессами. Пер. с англ. – М.: Альпина Бизнес Букс, 2007.
Скачать приложение Файл:Приложение.doc
Вклад участника
 Обратная связь Автору
Обратная связь Автору